Meta
天苍苍,野茫茫
全是一样的牛羊。
本文是一篇非常传统性质的Metric Learning文章。
啥样的metric比较好?
当然是Mahalanobis了,起码它比欧氏距离更general。
好了,既然我们知道了这个metric的形式,那么去learn它不就是一个很基础的数学问题了么。
注意,本文搞的是 有监督的情形。
应该能够发现一些可以借鉴的东西吧。
摘要
Metric Learning的nature决定了,对于large scale data以及data
for which classes overlap来说,非常困难。
本文提供一种方法:improving accuracy and scalability of any iterative metric
learning algorithm
也就是为现在的好多metric Learning的算法给小修一下,具体就是,改改抽样的策略,即class重叠的地方的sample抽样概率大一点。
恩,有监督的时候才能这么玩儿吧?
我要是无监督的咋知道乃们是重叠的????
Intro
很多ml算法依赖于距离或相似度的概念。但是这个measure非常依赖于在特征空间的数据分布。
首先提到,将这个分布或流行考虑进去的是无监督的。
如一开始的PCA,在这种manifold learning中:
the objective is to preserve the geometric properties of the original feature space while decreasing its dimension so as to obtain a useful projection of the data in a lower dimensional manifold, refer to e.g. MDS, ISOMAP, LLE, SNE (see [2] and references therein), or more recently t-SNE [3], a Student-based variation of SNE.
然后有监督的来了,即 class label用于 guide this projection, particularly by focusing on easing the prediction task (see e.g. Fisher linear discriminant analysis and its variants).
将data投影到新的特征空间,这个新的特征空间作为 原特征空间的线性组合。
当然,最近流行的是 直接在原空间学习这个distance (or similarity) measure,不需要投影了。
上面提到,manifold learning是无监督的。
而 metric learning uses some background (or side) information。如这篇seminal paper
E. P. Xing, M. I. Jordan, S. Russell, and A. Y. Ng, “Distance metric learning with application to clustering with side-information,” in Advances in neural information processing systems, 2002, pp. 505–512
这样,相似度的概念怎么搞呢?
对于监督问题,通过label得到;对于半监督,通过must-link and cannot-link,
or side information得到。
此处, $A$ 必须得是半正定的。由于 此限制有点强,有许多work都是围绕着 $A$ 来玩儿的。
metric Learning 非常重要的一步就是根据(class labels, relative constraints) 来定义 constraints。
很多算法都是随机选取一些满足这些constraint的paris或triplets。
作者对这种approach的批判就是,它可能没法focus到特征空间中的 重要区域 (如class的边界处)。
哈哈,这种pair的已经被批判好多次了。以前有篇文章说这种pair学习的是local structure
本文的approach:根据当前的metric 动态设定constraint的weight。
即,已经满足的很好的constraint的权值就小一点,没有满足好的constraint的权值就大一点。
作者强调,本文的approach并不局限于特定的metric learning 算法。
哎呀, approach比algorithm还general?
METRIC LEARNING AND RELATED WORKS
由于本文是有监督的,我就不仔细看了,摘几个感兴趣的点吧。
这一节除了将triplet 和pairs的approach之外,还提到一个Maximally Collapsing Metric Learning algorithm,它利用一个非常simple geometric intuition:一个class中的所有点都要map到特征空间的同一个点,当然,不同class的点都要map到不同的点。
作者接着又扯到一些跟boundary points相关的文献,借此强调了一下,本文的approach即考虑到了边界点,又考虑到了距离边界很远的点。
最后强调了本文搞的是global metric learning algorithms,只学习一个 $A$ 就行了。
本文算法
哦,我突然乱入到一个有监督分类的paper中,好不适应……
看了一下篇幅,算法部分不到一页半,和我水平差不多嘛。
本文的approach的两大特点:instance selection, and the principle of boosting。
进来一个input instance,我都要给你个weight,这个weight每次迭代的时候都要更新。
详细点就是,根据当前误差计算一个loss,根据这个loss来更新weight。
作者 搞出来一个loss function 能够 adapted to the different type of constraints。 这些constraint一般可分为四类: Class labels,Pairwise labels,Triplet labels,Relative labels。这四类咋分的?根据考虑instance的数目,分别是1到4.
定义好loss之后,就是大招了,即根据作者的经验和intuition,由于在class重叠的地方,metric 学习非常难,因此,这些地方的抽样得更频繁一些。
本文的算法就是这么多了。
式子我就不想放了。
再总结一下:本文的算法就是,先定义一个loss,这个loss定义的关键在于一个相似度阈值 $\gamma$. 然后根据和这个loss来计算这个instance下次迭代的时候被sample到的概率。
就是这么简单。
下图就是iteration的过程中,每一个instance的权值变化情况。
红色表示大,黄色,小。
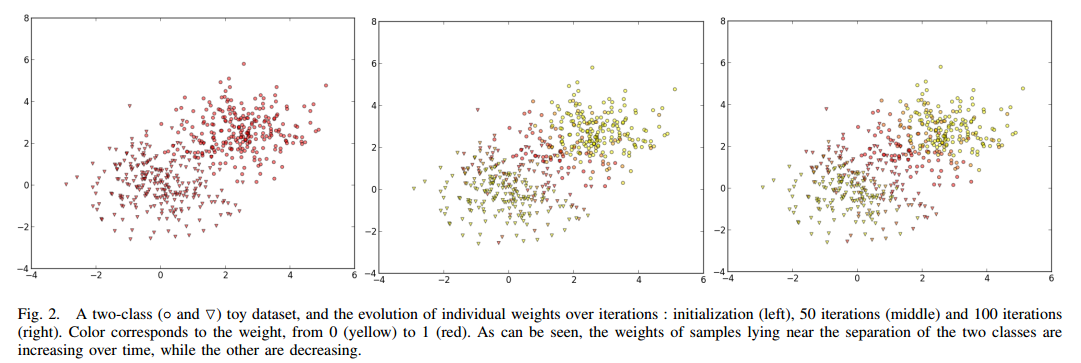
看来还是非常excited的。
下面就是algorithm的summary:

总结
这个算法啊,其实就是作者在自己玩儿的过程中随便搞出来的,一点都不复杂,甚至不需要动脑子。
康肃问曰:汝亦知射乎?吾射不亦精乎?
翁曰:无他, 但手熟尔。
所以啊,信息量大的地方就是intro了。