扯扯淡
这几天杂事比较多,重新装机花了我两天时间,另外自身的调节也没做好,差点又lost myself了。
好了,好好看论文,多思考。
前言
现在 metric learning 的best approaches
利用soa的NN得到一个embedding function,以最小化某种loss [19, 30, 27, 9],
作者钦定它们 无法考虑 global structure of the embedding space,因为它们的loss 都是定义成 training mini-batch 中的 pairs or triplets
作者不用这些pairs or triplets,因此 作者的 algorithm is aware of the global landscape of the embedding space。
以下是作者的work,其中第二点是技能树
- 我们要学习到一个 直接优化距离指标NMI 的embedding function
- 使用 structured prediction framework [34, 14] 来确保 ground truth clustering assignment的score 高于 其他的clustering assignment
- 搞了三个数据集: CUB200-2011 [36], Cars196 [18], and Stanford online products [29] datasets for clustering and retrieval tasks.
总览
- 干了啥:搞了一个新的学习方案,优化 deep metric embedding with the learnable clustering function and the clustering metric (NMI) in a end-to-end fashion
within a principled structured prediction framework - 定位:这篇文章可以说就是设计loss的。
在3.2节结束的地方,作者提到这个loss的特殊之处: 小的类内variance,同时类间隔足够远(通过NMI metric项实现) - 作者的卖点
- 声称:the algorithm is aware of the global landscape of the embedding space。
- 和三个soa的算法比起来,不需要将数据准备成pairs
不过我还没看明白咋实现的,这东西隐含在loss的形式中了,得好好看啊。
看到实验细节部分,就是用Tensorflow搞几个式子嘛。 即便是端到端的,图像的各种初级预处理也得有,如都crop成 227 × 227。
Related work
在 deep metric learning 的seminal work [8, 4] 中,最小化类内pairwise distance,最大化类间pairwise distance。
但它用的是绝对距离,而作者说对于大多数任务,relative distances matter more.
因此好多不同的 损失函数 搞出来了。
作者重点提到一篇 CVPR, 2016,Deep metric learning via lifted structured feature embedding,它将所有的 negative pair 都比较一下。
Github代码
这一篇一定要看一下。
还提到两篇clustering的:
- [10] J. R. Hershey, Z. Chen, J. L. Roux, and S. Watanabe. Deep
clustering: Discriminative embeddings for segmentation and
separation. In ICASSP, 2016. 它用的是Frobenius norm,缺点是suboptimal, since it ignores the fact that the affinity matrix is positive definite. - 为了克服上面的那个缺点,matrix backpropagation Training deep networks with structured layers by matrix backpropagation. In ICCV, 2015.
将 affinity matrix 投射到 a metric space where Euclidean distance is ppropriate
作者的方法
general outline
两个图镇楼:
在图二中,橙色的positive pair被其他类的 example隔开了。
the attractive gradient signal from the positive pair gets outweighed by the repulsive gradient signal from the negative data points (yellow and green data points connected with the red edges).
因此同一类内的example在embedding space中有可能离得很远。
在图三中,加粗的几个点是聚类中心,由于本文的算法 learns to embed points so as to minimize a clustering loss ,因此类内variance尽量小,类间距尽量大。
作者根据这俩图钦定了:
the algorithm is aware of the global landscape
of the embedding space, it can overcome the bad local optima in figure 2
facility location problem
在已知 inputs $X_i$ 和 an embedding function $f(X_i;\Theta)$ (将 $X_i$ 映射到一个 $K$ dimensional space)的情况下,根据 landmark 对这些点进行压缩,别看公式核名称那么玄乎,其实就是 单个类的类内variance,即每个点与最近邻的距离之和。
\[F(X, S; \Theta) = -\sum_{i \in |X|} \min_{j \in S} ||f(X_i; \Theta) - f(X_j; \Theta)||, \label{eqn:facility}\]其中 landmarks
$S \subseteq \mathcal{V}$,, $\mathcal{V} = {1, \ldots, |X|}$ is the ground set。
注意 :
- 这个facility location problem 用作整个 deep metric learning 的一个环节。
- 最大化 $F$ 其实就是最小化类内variance。
Structured facility location for deep metric learning
作者搞出来一个oracle scoring function,用于测度已知 真实类标 和 embedding参数 时候的 clustering quality。

这个东西就是所有类的 类内variance 之和。
在前言中,作者提到 structured prediction framework _ 能确保 _ground truth clustering assignment的score 高于 其他的clustering assignment
现在我们的 需求 是,要确保不太好的 clustering assignment 的score 距离 oracle 的很远,当然我们期望的 predicted clustering assignment 的score 要距离 oracle的近一些,因此设计 structured loss function 如下:

作者钦定这个loss的功能如下:
oracle clustering score $\tilde{F}$ is greater than the 至少比其他 cluster assignments $g(S)$ 的 clustering score $F$ 大一个 structured margin $\Delta\left(\mathbf{y}, ~\mathbf{y}^*\right)$.
如果真是这样的话,公式6就得这么理解:这个式子必须得是正的。
好了,整体框图如下:
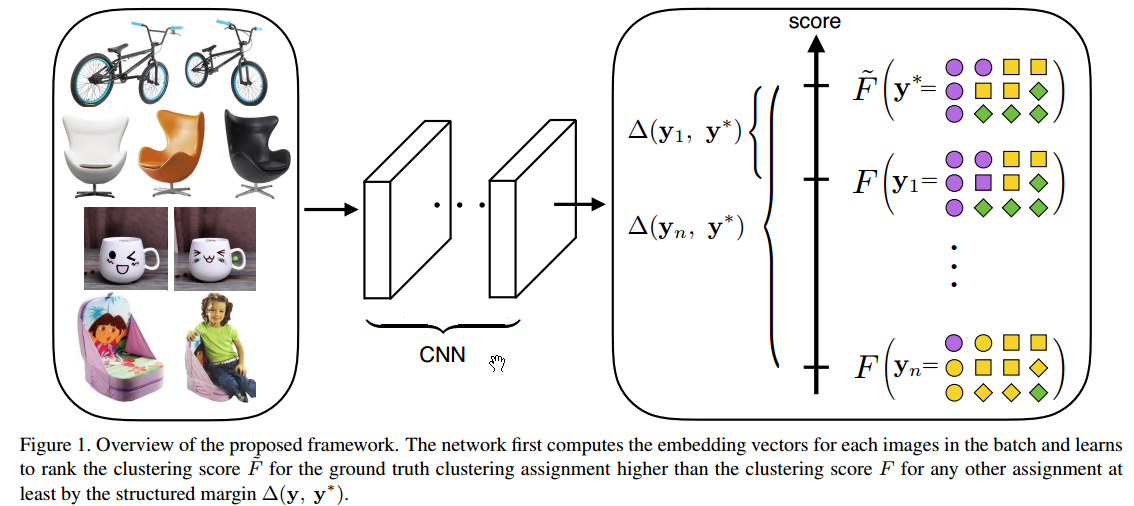
Backpropagation subgradients
NN的训练离不了SGD,那么关键步骤就是6式的derivative了:

其它两项很好算:

下面就是如何求解6式了。
Loss augmented inference
由于第一项 $F(X,S; \Theta)$, is a monotone submodular function in $S$,并且第二项,即 margin term 相比第一项来说很小,故这俩的和依然很接近 submodular, 因此可以用 greedy Algorithm 1 来解。
而且有文献表明,对于approximately submodular functions, the greedy algorithm效果也不错。

注意:这里要求真实类标是已知的!
对于算法1的解释:
In each step, it chooses the element $i^*$ with the best marginal benefit.
啥意思?就是说,每次我们都要找到一个点,使得marginal 的增量最大(其实不仅仅是marginal 增量)。
当然,由于 $A(S)$ is not entirely submodular,还可以将这个 greedy solution 用 local search 给 refine 一下。
这个算法跟 partition around medoids (PAM) [15] algorithm for k-medoids clustering 很像,其实就是将当前的聚类中心替换为该类的其他点,然后找到增量最大的点。

Implementation details
计算loss的时候对embedding vectors 进行 $\ell_2$ normalization
算法二可以用随机初始化,也可以用算法1初始化,后者效果好一点。
网络结构细节:
Inception
[31] network with batch normalization [11] pretrained on
ILSVRC 2012-CLS [23] and finetuned the network on our
datasets.
有文献表明 embedding size 对于实验效果影响不大,因此将其固定为 64. 即64维。
其他参数:
We used RMSprop [32] optimizer with the batch size m set to 128.
For the margin multiplier constant γ, we gradually decrease
it using exponential decay with the decay rate set to 0:94
感受和总结
感受
上周处于各种调整期,又重装系统,因此花了将近一周的时间才将其看完。
当时看的时候对这个领域很陌生,原因就是很多common的东西不知道,如这个圈子咋玩儿的,一般都有哪些方法,deep learning 的轮子不熟悉等。
现在回过头来看,发现也就那样,都是在现成的框架里跳舞。
embedding function的学习其实就是学习一个映射,再用NN的paradigm就是用SGD等学习一堆NN参数。 好了,NN的梯度从哪儿来?你就得设计一个好的loss了,这个loss就反映了你的问题的characteristic,这个loss形式的好坏indicate了NN能否从你的loss中得到足够有用的information,进而学习到好的embedding function。
总结
这篇文章应该作为一个引子,进入这个领域。
它的试验中提到三个soa,其中一个我发现有github的代码。
这篇文章提到好多cvpr,iccv等的文献,都可以看一下。
这些文献说明作者的积累。
好好干吧,![]()