别人的阅读笔记
https://zhuanlan.zhihu.com/p/27614220
http://www.cnblogs.com/everyday-haoguo/p/note-PredictingNoise.html
小总结
目标是用无监督的方式进行特征学习。
但无监督的话一般需要避免trivial解。
本文很像另外一篇文章:
Yang, Bo, Xiao Fu, Nicholas D. Sidiropoulos, and Mingyi Hong. “Towards K-Means-Friendly Spaces: Simultaneous Deep Learning and Clustering.” In PMLR, 3861–70, 2017. http://proceedings.mlr.press/v70/yang17b.html.
即通过要求网络能够重建输入,从而保证能够避免trivial解。
而本文的限制更弱一些,即随机生成一些(互不相同的)点作为目标函数值,让构成input-output pair,然后让网络去拟合这些数据对,这就是论文题目 Predicting Noise 的由来。
另外,估计作者试过了,仅仅随意生成一些噪声作为目标函数值效果不太好,因此让网络在训练的时候去选择目标函数值,即我生成的噪声点的数目大于input 点数,即还需要学习出来一个选择矩阵 $C$。
细节
首先是损失函数,初步选择为
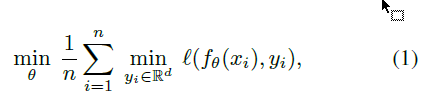
如果采用有监督常用的softmax的话,计算量就比较大(估计是因为所有的目标输出都要参与到计算中),因此采用了常用的 $l2$ :
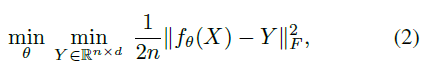
这样就能per sample了,即making its computation independent of the number of targets.
至于选择矩阵的表示和优化就比较麻烦了。
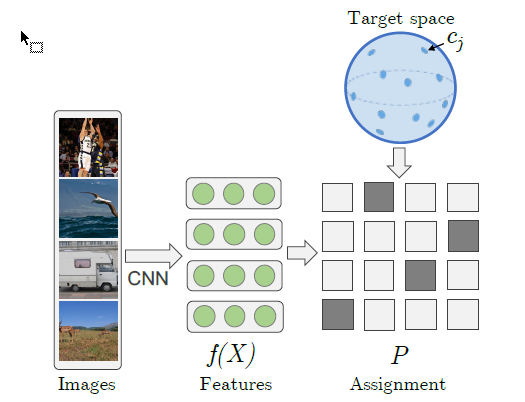
基于上面提到的原因,先从一个 $d$ 维 $l2$ 球中均匀抽取 $k$ ( $k \le n$ )个点, 这些点组成一个 $k\times d$ 的矩阵 $C$.
作者做的就是 fixing a set of k predefined target representations and matching them to the visual features.
随之而来的一个问题就是定义一个 ${0,1}^{n\times k}$ 选择矩阵,$P$ (最后它得通过训练来得到),即它的每一行只有一个1,同时我们还得限制每一个input point对应的y不一样,因此每一列只能有一个1,恩:
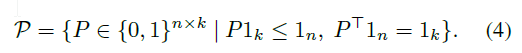
最后变成这个样子:
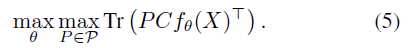
随机优化:

意料之中的是,就像普通的深度聚类,优化聚类目标函数与NN调参交替一样,这边也是P的更新与NN调参交替。
另外关于矩阵P的优化,作者是分块优化的,具体我就不看了。
至于学习到特征之后的事,先不看了。