简介
这篇文章虽然是关于Computing with Words的(CWW),扯的都是很宏观层面的东西。
还是有一些非常general的东西在里边。
CWW简介
Zadeh先生在96年提出来的。
输入是word,然后用fuzzy set转换成mathematical representation,再经过 一个 CWW engine 转化成 另一个 fuzzy set,最后再转化成一个word
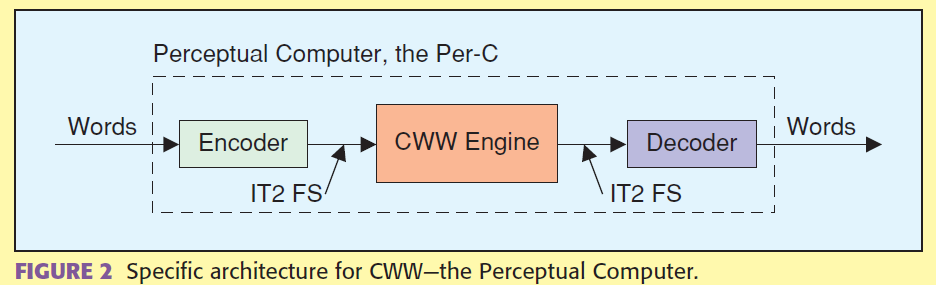
具体细节
validation
Turing Test:a test to assess a machine’s ability to pass for a human being。
一定要有data,没有那就编造数据或者不用数据,直接设计CWW engine。
模型选择
由于一个word对不同人的意思不太一样,因此我们的 fuzzy set 模型必须得capture word的不确定性。
可以用type-1 (T1) FS or an interval type-2 (IT2) FS。
至于General type-2 FSs,作者强调,General type-2 FSs are presently excluded, because they model higher degrees of uncertainty, and how to do this is totally unknown
那么我们就有两者不同的approach。
- 用T1 FS来设计,and see if it passes a Turing Test. If it does, then it is okay to use such an FS model.
- 在设计CWW engine之前,在T1 FS model和IT2 FS model之间进行选择。
第一个approach无需多言,至于第二个的选择,涉及到scientific的定义。
20th century scientific philosopher, Sir Karl Popper 提出了falsificationism(证伪)的概念,用于 establish if a theory is or is
not scientific.
如果一个theory能够被一个反例证伪,那么那就是scientific的。
A theory is scientific only if it is refutable by a conceivable event. Every genuine test of a scientific theory, then, is logically an attempt to refute or to falsify it, and one genuine counter instance falsifies the whole theory.
这个很有意思,我的理解是:宗教也可以被这么解释,你永远无法用特例证明这个神存在,或者不存在,也就是没有反例,所以人家就不是scientific。
对于证伪,Popper的意思是,如果一个理论和某些经验观测不相符,它就是scientific。
相反,如果和所有的观测都相符,就是unscientific。
一个scientific theory可以是对的,也可以是不对的,但一个incorrect scientific theory is still a scientific theory。
作者的结论:a T1 FS model for a word is an incorrect scientific theory。
理由是:一个 T1 fuzzy set A for a word 由一个隶属度函数 well-defined.
但明显是应该有uncertainty的,因此it is a contradiction to say that something certain can model something that is uncertain.
In the words of Popper, associating the original T1 FS with a word is a “conceivable event” that has provided a “counter-instance” that falsifies this approach to fuzzy sets as models for words
而IT2 FS model允许我们model 一阶不确定性。
因此
IT2 FS is a scientifically correct first order uncertainty model for a word; and, in the future the scientific correctness of an IT2 FS model may be falsified by a more complete T2 FS model because measurements can be made about words.
An objection may be raised that a fixed T1 MF also applies to an IT2 FS model 。
这时候就有问题了,只要一个IT2 FS model的参数确定了,关于IT2 FS的不确定性也就不存在了。
这时候,我们需要指出,this objection is incorrect because the IT2 FS is a first-order uncertainty model, i.e. at each value of the primary variable the MF is an interval of values.
可以类比分布函数。即,一个分布的参数确定以后,我们并不能说它不是一个概率模型了。
Occam’s Razor
模型定了,但是参数咋定,mf的参数,defuzzy的方法等,使用Occam’s Razor。
when you have two competing theories which make exactly the same predictions, the one that is simpler is the better
划重点,本原则并不是”keep it as simple as possible.”
如果两个或多个competing theories that lead to different predictions. Occam’s Razor does not apply in that case, because the results that are obtained from the competing theories are different.
当然模型再simple,你也得想过好才行,即受到Turing Test的约束。
结论
本文站在制高点看待问题,权当好玩儿的文章读一下吧。
收获:
- scientific的定义:能证伪
- Occam’s Razor的正确理解:有相同预测的模型之间取简单的