一篇NIPS 2016,非常理论的文章。
摘要
研究对象
online [5] and mini-batch [16] k-means variants
通过stochastic approximation来scale up k-means 的两大算法,现在主要用于
large-scale clustering and unsupervised feature learning
研究结果
首次证明,不管从哪个 initial solution 出发,都会以 $O(\frac{1}{t})$ 收敛到一个局部最优。
还有,只要数据集是 clusterable的,在用一个 simple and scalable seeding algorithm初始化的时候,mini-batch k-means converges to an optimal k-means
solution at rate $O(\frac{1}{t})$ with high probability。
Intro
对于在大规模数据集上的聚类,由于每一次的iteration的时间都是 $O(n)$ ,因此不太好啊。
To scale up the centroid-update phase,一个可行的recipe就是 随机逼近。
the overall idea is:
at each iteration, the centroids are updated using one (online [5]) or a few (mini-batch [16]) randomly sampled points instead of the entire dataset.
本文的主要贡献就是证明了 $O(\frac{1}{t})$ global convergence of stochastic k-means。
关键思想是 追踪当前聚类结果与所有局部最优的距离。
就是下图表面了stochastic k-means against batch k-means on the RCV1 dataset:
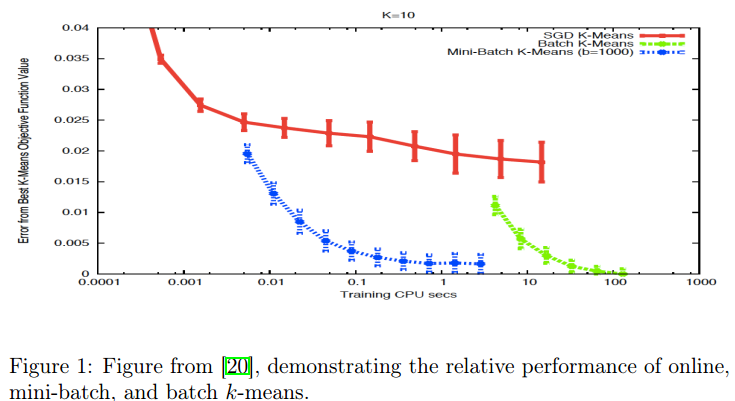
这就激发了作者想要characterize the convergence rate of stochastic k-means。探究为啥有局部极值,以及mini-batch size的影响等。
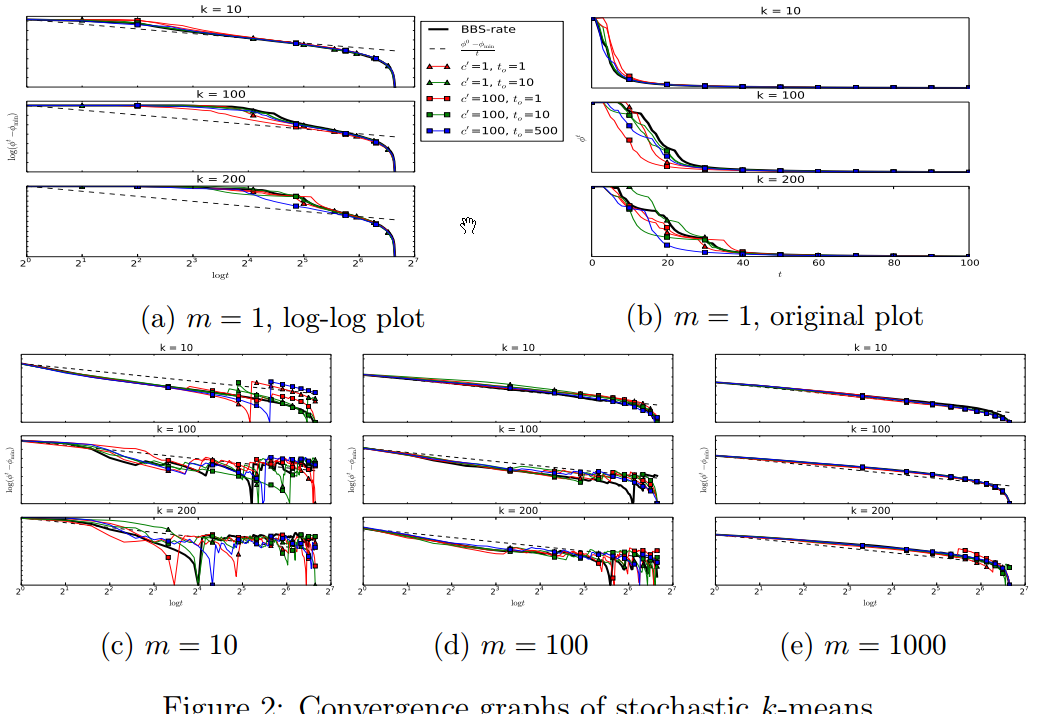
实验部分
数据集:RCV1 [12]。804414 newswire stories,每一额story 都是一个47236-dimensional sparse vector。
收敛图,暂时看不懂,以后再看: