前言
一个R包pdfCluster对应的paper。
基本思想:数一下pdf的local mode的数目
具体算法
怎么数呢?
一个基本的想法就是将pdf的曲线横着切一刀,然后数一下connected components的数目,但是该在那儿切呢?作者的方法是都切一下,当然为了好计算,是离散地取一些点去切。
更精确的描述如下。
初步想法
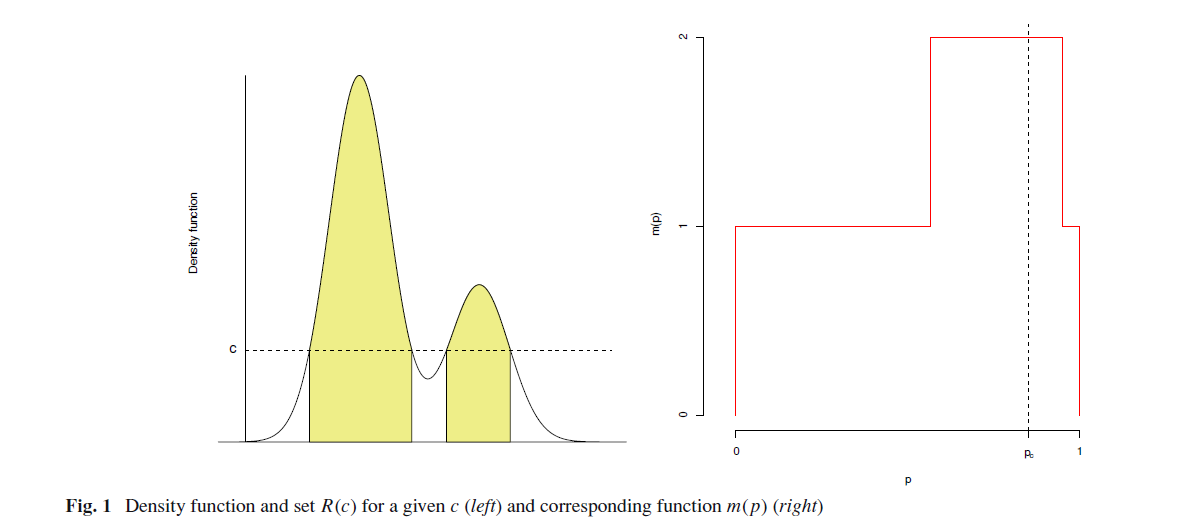
上图,左边是pdf,右边x轴是 $p_c$,即 pdf值大于 $c$的pdf的曲线下的面积, 纵轴 $m(p)$ 是此$p_c$对应的connected components的数目,
这样当 $c$ 由大到小时, $p_c$ 会从小到大, $m(p)$ 会先大后小
分别对应cluster的分离和merge
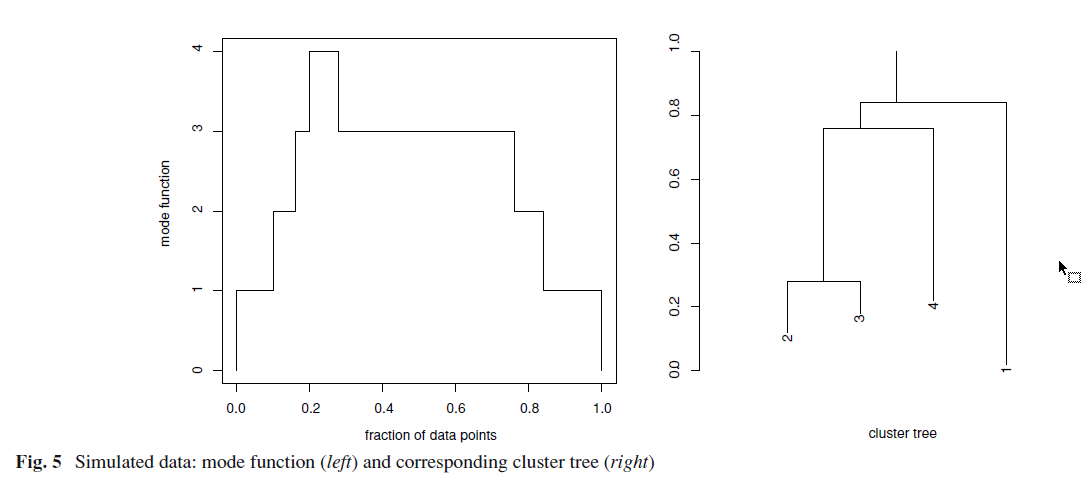
根据mode function就可以得到cluster tree
具体实现
mode function咋得到?
只能得到一个empirical的了,毕竟连pdf都是逼近的嘛。
作者使用了Voronoi tessellation and Delaunay triangulation的概念。
废话不说了,上图:
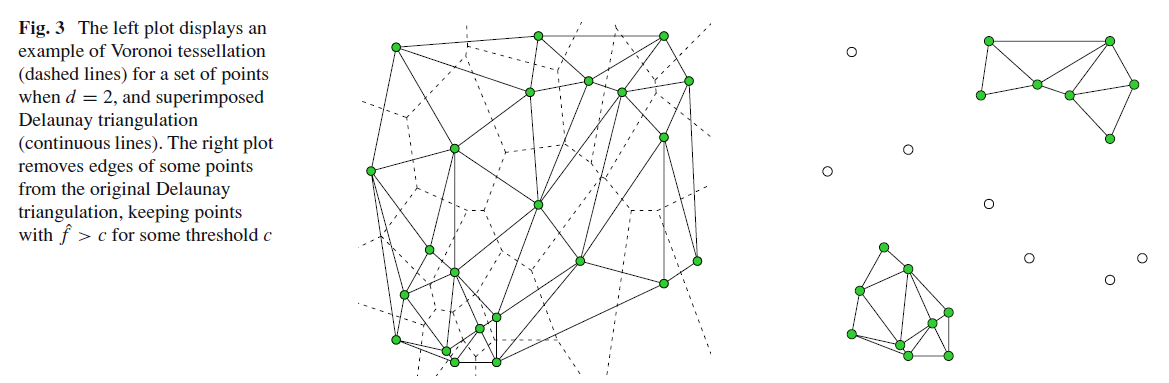
图中,虚线构成了Voronoi tessellation(估计是纯粹根据距离得到的,作者好像没有明说),然后得到实线部分的Delaunay triangulation
这个Delaunay triangulation就是用来构造mode function的关键
如果某一个triangulation的点的density小于 $c$,那么所有与它连接的edge都得干掉,这样就形成了上图右边的两个区域。
好了。就这样了。