总览
我看作者主页(哥大的Zhuo Chen),人家貌似一直在做这个,貌似还搞过公司。
看一下行文,貌似是很随意的一篇文章,应用很有趣,框架像是随手拈来的……
应用背景太多,这个东西是两方面的
- 聚类这么简单的思想也能干如此复杂的事
- 背景太多,不方便读者去消化
我决定粗略看一下应用吧,当然主体是第3、4页。
核心
$V = f_θ(x)$, 参数是 $\theta$, 由DNN实现,还是老规矩,求出loss对 $V$ 的微分就行了 (注意 $V$ 是最后一层)。
细节
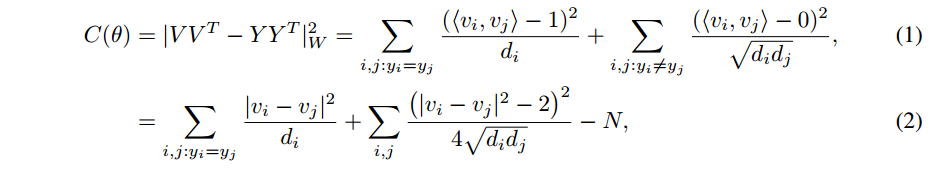
作者的符号notation不太好懂,我反正被绕晕了,$d_i$ 一会儿是vector一会儿又是一个数值,恩。
这个形式咋来的?有没有明显的借鉴,我见识太少,不得而知。
然而其物理意义却很显然:
这个目标函数将两个同一个partition中的点的内积 $<v_i , v_j>$ 强制接近1, 否则强制为0
从(2) 看出来,将 类内variance |v_i − v_j|^2 最小化,并且 while preventing the embeddings from trivially collapsing into the same point.
然后,作者将这个formulation和spectral clustering关联了起来,

翻译一下,将模型的affinity matrix和理想的affinity matrix的deviation由目标函数1、2表达了出来,看起来这个式子将所有点对都加了起来,但它的low-rank nature是很有效的。
我没有搞懂人家咋变换的……
然后3式的微分就是4式,这样就可以用来优化DNN了
谱聚类一般是做一个low-rank approximation of a full-rank model,本文的方法是直接优化a low-rank affinity matrix 。
结论
这个东西一时半会儿看不懂,没关系,等积累够了再回来看。
本文算法还是很清晰的,DNN那一部分也许是太general了,着墨不多,主体都放在了loss的design上面,而且这个loss的变化很吸引人,就是搞出一个low-rank的出来,还不是逼近的,好神奇。