Meta
这是一篇文章没有迭代训练DNN
先用DCNN提取特征,然后修改原始的相似度定义,最后采用层次聚类。
总括
将原始图像经过大名鼎鼎的DCNN,即DCNN的映射为: $f_{\theta}: \mathcal{I} \rightarrow \mathcal{X}$
然后再归一化 \(g: \mathcal{X} \rightarrow \mathcal{X}\) 得到deep representations 即
$X = g \circ f_{\theta}(I) = {\x_1, \ldots, x_{n_s}}$
本文所谓的Proximity-Aware其实就是考虑到点 $x_i$ 周围的点,即 K个近邻 $\mathcal{N}_K(\mathbf{x}_i)$
方法
先介绍传统的相似度定义
对于两个在单位球面 \(\{\mathbf{x} : \norm{\mathbf{x}} = 1 \}\) 的特征点 \(\mathbf{x}_i, \mathbf{x}_j \in \mathcal{X}\), 它们的相似度定义为:
\(s(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i^T\mathbf{x}_j. \label{eq:sim-original}\)
有了相似度,就可以定义距离了,即 $1 - s(\mathbf{x}_i, \mathbf{x}_j)$
这种定义的缺点:不够robust,即得要求你的目标数据(你的算法要用到这个 data 上)和训练数据的分布相当一致,而这个要求一般很难达到
因此本文要根据邻域结构来度量相似度。
本文的 Proximity-Aware Similarity 之初级版
先将上面的内积换个样式
\(s(\mathbf{x}_i, \mathbf{x}_j) = \dfrac{\mathbf{x}_i^T\mathbf{x}_j + \mathbf{x}_j^T\mathbf{x}_i}{2}. \label{eq:sim-proposed}\)
这样就可以将其赋予物理意义:两个特征点的相似度就是平均一下两个asymmetric measures:How similar is $\mathbf{x}_j$ from the view of $\mathbf{x}_i$ and how similar is $\mathbf{x}_i$ from the view of $\mathbf{x}_j$.
其中,$\mathbf{x}_i^T\mathbf{x}_j$ 可以理解为 evaluating $\mathbf{x}_j$ on hyperplane \(H_i = \{ \mathbf{x}: \mathbf{x}_i^T \mathbf{x} = 0\}\)
另外一个同理。
我们注意到 超平面 $\mathbf{x}_i^T \mathbf{x} = 0$ 只是一种很特殊的形式,如果更general一点,即能够包含 $\mathbf{x}_i$ 的邻域点信息,也就是说,这个超平面能够考虑到 $\mathbf{x}_i$ 的邻域点,那么我们就可以更robust地来计算相似度了
我们定义这个要寻找的超平面为: \(H_{\mathbf{w}_i, b_i} = \{\mathbf{x}: \mathbf{w}_i^T\mathbf{x} + b_i = 0\}\)
那么the asymmetric similarity from $H_{\mathbf{w}_i, b_i}$ to some set $S$ is defined as
\(H_{\mathbf{w}_i, b_i}(S) = \dfrac{1}{|S|}\sum_{\mathbf{x} \in S} [\mathbf{w}_i^T\mathbf{x} + b_i ].\)
好了,既然 $H_{\mathbf{w}_i, b_i}$ 的确定(即这个超平面的法向量和bias的确定)考虑到了 \(\mathcal{N}_K(\mathbf{x}_i)\) ,那么 这个超平面到 $x_j$ 的距离也得考虑到 $\mathcal{N}_K(\mathbf{x}_j)$,即
\(H_{\mathbf{w}_i, b_i}(\mathcal{N}_K(\mathbf{x}_j))\) 于是我们就得到了新的相似度的定义:
\(s_{PA}(\mathbf{x}_i, \mathbf{x}_j) = \dfrac{H_{\mathbf{w}_i, b_i}(\mathcal{N}_K(\mathbf{x}_j)) + H_{\mathbf{w}_j, b_j}(\mathcal{N}_K(\mathbf{x}_i))}{2}. \label{eq:sim-neighbor}\)
使之practical
由于 $s_{PA}$ 可能无界,因此需要加个非线性变换,如 $\arctan$ 或 $\exp$。
这样,我们就将定义两个neighborhoods相似度函数的问题转化为求超平面的问题。
另外我们期望的性质为:
$H_{\mathbf{w}_i, b_i}(\cdot)$ has a large value when evaluating on sets that are near $\mathcal{N}_K(\mathbf{x}_i)$, and has a small value otherwise.}
这个性质使得similarity measure to be locally geometry-sensitive (proximity-aware) but also adaptive to the data domain。
因此,作者决定,使用 linear classifiers to separate positive samples \(\mathcal{N}_K(\mathbf{x}_i)\) from their corresponding negative samples.
看图:
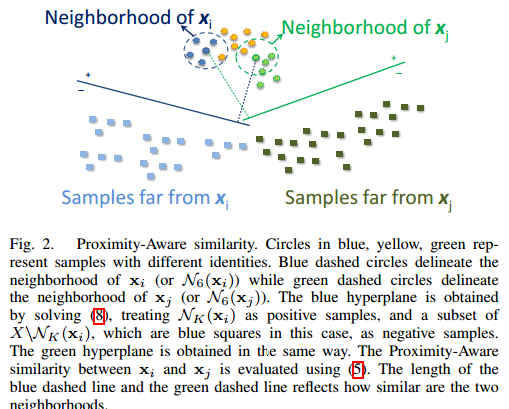
目标函数为:
\(\min_\mathbf{u} \dfrac{1}{2} \mathbf{u}^T \mathbf{u} + C_p \sum_{k = 1}^{N_p} \max[0, 1-y_k\mathbf{u}^T \mathbf{z}_k]^2 + C_n \sum_{k=1}^{N_n} \max[0, 1-y_k\mathbf{u}^T \mathbf{z}_k]^2\)
where $\mathbf{u} = [\mathbf{w}^T \quad b]^T$ and $\mathbf{z}_k = [\mathbf{x}_k^T \quad 1]^T$. We treat $\mathcal{N}_K(\mathbf{x}_i)$ as positive samples with cardinality $N_p$, and a subset of $X \backslash N_K(\mathbf{x}_i)$ as negative samples with cardinality $N_n$. $y_k = +1$ for positive samples and $y_k = -1$ for negative samples. The regularization constants $C_p$ and $C_n$ are given by $C_p = C \frac{N_p + N_n}{N_p}$ and $C_n = C \frac{N_p + N_n}{N_n}$.
相关的工作
本文的approach跟
The one-shot similarity kernel. In IEEE International Conference on Computer Vision (ICCV), 2009
很像,人家用的是LDA, 本文作者不用LDA的原因是,LDA有bimodal Gaussian prior assumption。
试验
效果很不错,不知道是DCNN本来就这么强了呢,还是本文的后续相似度定义的好呢,不得而知啊
不过既然效果好,能肯定的是DCNN的representation学习的好啊。