前言
这是一篇ICML17在审的文章。
精确设定regularization,从而将输出层调教成具有clustering意义的neuron。
本文的调教过程如丝般润滑,叹为观止。
摘要
光看摘要没啥有意思的嘛。
- 有一句,增加正则化项以encourage the neural network to reveal its own explicit clustering objective。没有人工钦点它的目标函数?一股清流啊……
- 由于寻找subclasses是无监督的,因此可以轻易变成半监督。
- 这个network能够naturally create sub-clusters under the provided main class labels.
我居心不良地揣测一下,作者非得扯上半监督,很明显是对无监督效果的不自信吧,待会儿看完文章再核实一下
粗略扫了一下实验部分,的确,无监督部分的实验的确需要更多的调教,效果还可以,当然没有半监督的好。
Auto-Clustering Output Layer
序言
初看这一章的序言,感觉很牛逼啊。
一个ANN,在优化classification objective的时候,通过ACOL这个输出层,能够find subclasses within these classes.
作者称之为
perform a secondary task - unsupervised clustering - while the primary task -
supervised classification - is being carried out.
这么搞为啥还能成为无监督?因为我们的data并没有subclass的信息,即subclass exploration这一步是无监督的。
这样整个learning procedure就是半监督了。
插一句:
我早就感觉可以先分类再聚类,但没有作者想的这么完备,能够将有监督“隐藏”地这么完美,水平真的很高。
作者举了个例子来说明这个半监督的牛逼之处:只要你的data能够变成二分类问题的data,就可以由本文的算法搞定。
试想,我们要分类 每一个数字和字符(digit and letter),这时候算法只需要知道一点点信息,即这个训练数据是数字还是字符啊,然后算法训练好以后,还顺带学习好了对每一个数字的分类,即0和1的分类,这个算法简直了……
不急,还有更牛逼的,如果嫌上面例子的监督信息太多,那好,还可以将原数据做个transformation,这样就有两类了:原数据,变换后的数据。
本算法并没有使用竞争学习(competitive learning),它用的就是普通分类问题的error correction learning,即BP。
而且没有显示的聚类目标函数。clustering objective是网络自己reveal出来的,当然,世界上哪有这么美好的事,choosing this objective will be crucial in order to obtain accurate clustering。
Output Layer Modification
看到这个结构,我瞬间想起了FMM,FMM用很多box来表示一个class。不同的是,FMM的每一个box并不能exactly或大多数情况下不能represent一个cluster。
还有一个问题,K值如何确定?这些在clustering中未解的问题在这里依然未解。
关于Learning的过程,作者强调,ACOL 并不会剧烈改变Network的feedforward and backpropagation mechanism,也就是说,不要怀疑俺,俺还是DNN啦。
聚类原理
就是要得到:specialized and equally active softmax nodes
至于原因,则很简单。
先看网络结构:
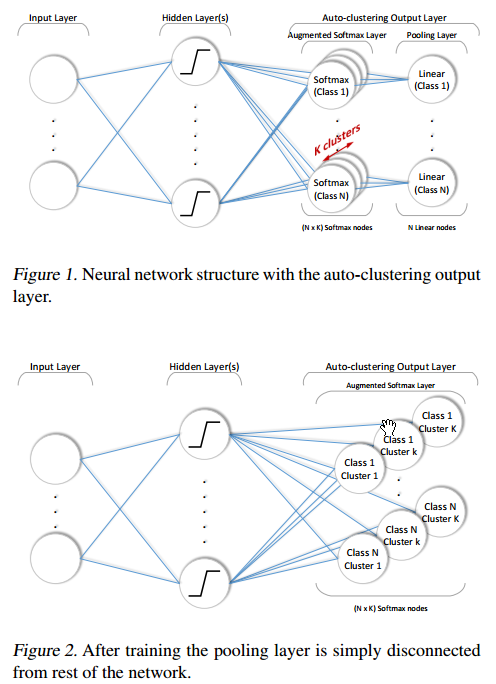
即,每一个classs都有K个cluster,我们训练的目的就是,当分类任务完成以后,每一个class的这K个node都得specialize成一个cluster。
举个例子,在本文的实验中,minist数据集上,我们将小于5的数字的label设为0,反之则为1,这是个information非常少的分类问题,当分类问题搞定以后,分类为0的那五个node就得分布specialize成识别0-4这五个数字的cluster。
这个咋实现?
我们先一步步地分析吧。
首先这个网络结构中,labels are now implicitly applied to multiple softmax nodes, 即 将one-hot encoded vector at the output转换成K-hot encoded vector at the augmented softmax layer,这个一定要理解,它是后边的基础。
这K个node同时收到label and the prediction的误差信号,然后backpropagate 回去。
这个结构为啥能 create clusters?
因为ACOL层和前一层之间多引入了 $NKN_{L-1}-N*N_{L-1}$ extra trainable weights。
现在ACOL的每一个softmax node都和前一层有 $N_{L-1}$ 个单独的权值。
由于 权值初始化是随机的 ,训练结束后每一个 softmax node很有可能只specialize到 a subset of the samples of that class。
但要想实现这个美好的目的,必须得这个 训练过程进行控制。
作者又分析了一下,dropout没法进行控制。
我们再明确一下,这个过程应该咋控制,首先 这些node得specialize,但又不能老是让一个node处于激活状态,即大家都得有机会激活。
这个可以通过对cost function增加regularization terms来实现。
好了,具体的实现也没那么难。
先定义一个Coactivity,即为了保证只有一个node对这个input example激活,其它node的激活必须为0(或尽量小),具体操作可以是:每两个不同的node的激活乘积,最后再加起来,让它们尽量小,这就是公式9.
但,正如上面分析的那样,公式9最小化了,很有可能一直都是那一个node处于激活状态,即,coactivity only supports the dominating cluster problem。
咋办?就得定义另外一个regularization term,它和Coactivity很像,但有一点不同。
我们得最大化这一项,即让每一个node对所有example的激活之和,最后加起来,最大化,但这个东西很有可能无界,咋办,把它normalize一下,变成Balance参数 $\beta$,这就是公式13.
现在Balance参数归一化了,但Coactivity还没有归一化,咋弄啊,Coactivity归一化之后就是Affinity $\alpha$ (公式14),但是这个归一化过程会损失一些东西,即Affinity变小之后就没法继续传递误差信号了,这时候我们就得用上Coactivity了。
这就是公式16.
当然,作为一个加分项,还么一再加一个 $L^2$ norm,这就是最终公式17了。
一些必须搞清楚的问题。
本文为何强调要分为两类,换句话说,为啥要有classification?
这个问题可以从第八页的实验部分找到答案,在没有人工label的时候,作者将原数据做各种变换,如水平镜像、九十度旋转等搞出其它class的数据,硬生生造出一些label
Our intuition is that transformations should challenge the network in order to force it to focus on the details of input. For example, distinguishing a digit 0 from its other 7 transformations is a difficult task, as a result we have obtained good clustering performance. However, shifting the images to generate pseudo-classes creates an easier classification task, which results in bad clustering performance
翻译一下:作者的intuition是,这些“不同class”的数据必须和原数据有大的差别,很明显我旋转180度,6和9就很难区分了,因此差别很大。这样 能够让network focus on 输入数据的detail上。
K过大的时候有啥现象发生
在第八页右上角,作者提到,对于10个数字的识别,每一个class如果令K=20,那么会有4个node为空,即没有任何一个input sample能够激活它们。
本文的算法除了K的设定是玄学以外,还有其它地方很玄么?
有,在实验部分,很明显可以看出来,我们要在恰当的时机,将 $c3$ 设为非0.
在3.1.2节(第七页右下角),作者提到,当K=5,10的时候,有差别。即K越大,affinity 降的越慢。因此要等到affinity 降到很小,得需要更多的epoch,这就意味着,我们必须时刻检测affinity 的数值,等到它很小了,才能让 $c3$起作用。
总结
本文的算法development过程很畅快,normalization非常巧妙。
但这个依然是CV圈儿的聚类,并不是general的。