Camera Models and Fundamental Concepts Used in Geometric Computer Vision

• 粗略读后感
• 摘要
• Introduction and Background Material
  • Introduction
  • Background Material
    • Plücker coordinates
    • Lifted coordinates
• Technologies
• Camera Models
  • 全局模型
  • 局部模型
  • 离散模型
• Epipolar and Multi-view Geometry

以下来自：
Sturm, P., 2010. Camera Models and Fundamental Concepts Used in Geometric Computer Vision. FNT in Computer Graphics and Vision 6, 1–183. https://doi.org/10.1561/0600000023

粗略读后感

这篇论文适合了解了所有模型后，猎奇用。
不适合学习相机模型用。

摘要

鉴于 geometric computer vision (“structure-from-motion”) 的 算法和理论研究 经常在没有突出 common underlying principles 的情况下被 re-developed，本文要综述：

1. 图像获取方法
2. camera model， 并指出不同模型之间的相似性。
3. 还有不同相机模型的 极线几何和多视几何(epipolar and multi-view geometry)。
4. 标定和自标定算法。

最后描述 geometric computer vision or structure-from-motion 的 fundamental building blocks：

1. 极线几何
2. 位姿和运动估计
3. 3D scene modeling
4. bundle adjustment.

Introduction and Background Material

Introduction

相机模型，或者说是 ` a computational model for a camera`， 告诉我们两个信息：

1. 如何将 3D 点投影到 image
2. 还有back-project，即从 image 到 3D

本文意识到，目前相机模型的分类是不太准确的，因为即使非参模型 其实也是有参的，例如camera rays的坐标。
因此本文分为三类模型：

1. A global camera model
   任何参数的改变都会影响所有视角（ field of view ）的投影函数， 例如经典的 pinhole 模型，以及 大多数鱼眼模型
2. A local camera model
   每一个参数只和视角的某一个子集（a subset of the field of view）的投影函数有关，例如，定义在image或者 field of view 上的多边形区域上的“piecewise-pinhole”模型。
3. A discrete camera model
   每一个不同的像素点都有对应的参数。当然，一般只定义一部分像素点的参数，然后通过插值得到其他像素点的参数。

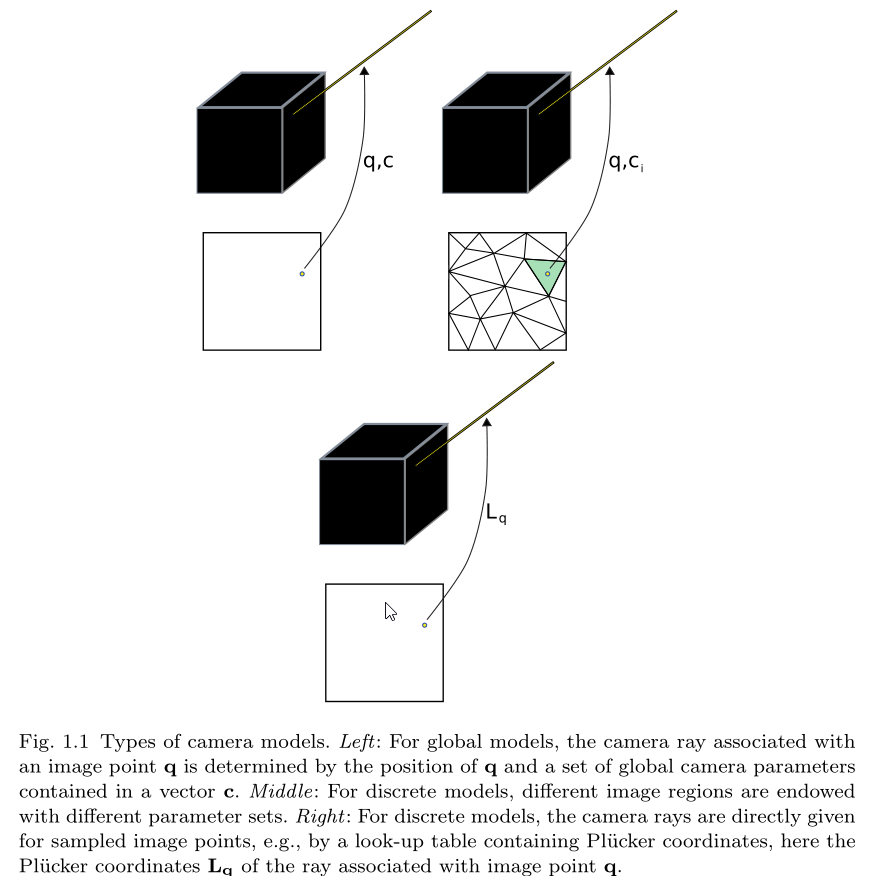
图中，第三个图像就是离散模型，其 camera ray 就是通过 Plücker 坐标的查找表得到的.
上面讲到了相机模型由两部分组成, 本文使用 back-projection来表示相机模型,也就是从像素点到相机光束(camera ray)的映射.

Background Material

Plücker coordinates

首先是 3D 空间中 line 的表示：Plücker coordinates， 也就是说，一个line 可以由一个六维的矢量来表示。
本文讲的比较粗略，详细资料可参考： Notes on Pluc¨ ker Coordinates。
这个坐标的好处是什么呢？

1. 这条直线的 direction 矢量 恰好是Plücker coordinates的前三个元素组成的矢量。
2. 这条直线与坐标系原点构成的平面的法向量（也就是the moment of the line） 恰好是Plücker坐标的后三个元素组成的矢量。

经过这个line的 direction 矢量 和 moment 矢量能够给 这个line上的点施加两个限制，并最终简化成一个线性方程。

Lifted coordinates

然后是Lifted coordinates。
本文讲的比较粗略，我参考了： Epipolar Geometry of Central Projection Systems Using Veronese Maps
也就是：

Barreto, J.P., Daniilidis, K., 2006. Epipolar Geometry of Central Projection Systems Using Veronese Maps, in: 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition - Volume 1 (CVPR’06). Presented at the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition - Volume 1 (CVPR’06), IEEE, New York, NY, USA, pp. 1258–1265. https://doi.org/10.1109/CVPR.2006.111

在代数中，一个标准技巧就是通过寻找一个 embedding 将问题弄到高维空间，从而使非线性问题转化为线性问题。
上面的参考文献又指出另一个文献：

J. G. Sample and G. T. Kneebone. Algebraic Projective Geometry. Claredon Press, 1998.

Technologies

这一节讲了各种类型的相机的构成。

Camera Models

首先介绍一下Back-projection 和 forward projection的区别。
二者互相定义，但很多情况下，只有其中一种形式比较好表示。
一般来说，back-projection 更加容易进行 formulate。例如，当我们使用点坐标的有理多项式函数来表示相机模型的时候，使用back-projection就会非常直接，然而使用 forward projection就会发现，映射到同一个像素点的 3D 点组成的是一个曲线，也就是 curved
“camera rays”。

Back-projection 一般有两种 formulation：

1. 根据像素点计算出 camera ray的两个点： point at infinity $B^i$， 以及 a finite point $B^f$。
   此时，
2. 根据像素点计算出 camera ray的Plücker coordinates $B^l$

全局模型

首先是 Pinhole model， 其image points 和 ray directions的关系为：
\(q\sim KB^i\)
其中 $\sim$ 表示两边差一个scale， $K$ 为内参矩阵。

对于经典的 polynomial distortion models 来说，distortion corrected image points 就对应于普通 pinhole model 的像素点，和 camera ray的关系为：
\(B^i \sim K^{-1}\left(\begin{array}{c}x_u\\ y_u \\1 \end{array}\right)\)

至于其他模型则形式更复杂一些。例如Polynomial and Rational Polynomial Models。

局部模型

包含Two-Plane Model等模型。

离散模型

略。

Epipolar and Multi-view Geometry

略