-->

High-precision localization using visual landmarks fused with range data

Posted on Dec 18, 2018 By Marquis

以下来自：
[1]ZHU Z, CHIU H-P, OSKIPER T等. High-precision localization using visual landmarks fused with range data[C]//Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on. IEEE, 2011: 81–88.

Simultaneous 3D Model and Visual Landmark Database Construction

  1. 用 LIDAR 扫描，通过 ICP 处理重叠的点，这样就生成了点云。
  2. 生成 visual landmark: 对于每一次的扫描，得到accurate camera pose，2D features（图像特征），以及 3D location

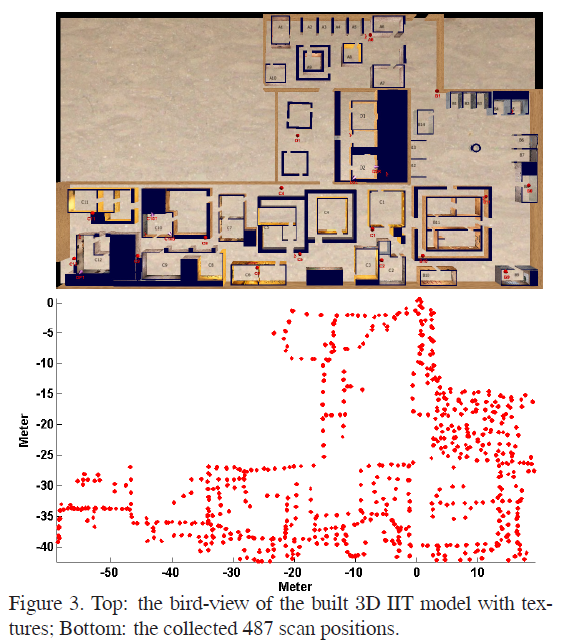
本文建立了包含 487 次扫描的 visual landmark database，大约 1.8GB。

下面将介绍 Localization With Landmark Matching

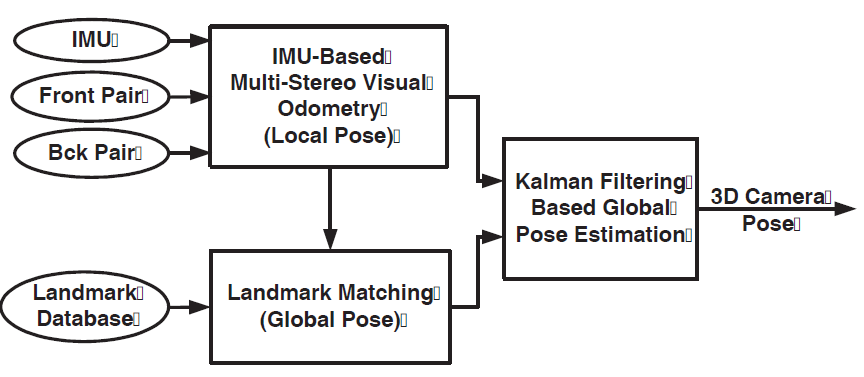
总体介绍

三个模块：

  1. IMU fused multi-stereo visual odometry,
  2. landmark matching
  3. Kalman filtering based global localization estimation

首先加载 visual landmark database。
然后系统获取传感器数据，即

  1. synchronized stereo image pairs
  2. IMU measurements。

这俩数据送到 visual odometry module 中。

  1. 从图像中提取 Harris corners ，并从 Harris corners 中估计相机的初始姿态（initial camera pose）。
  2. 上一步得到的 initial camera pose 再和 IMU measurements 进行融合，得到相机姿态（当然是局部坐标系的位姿啦）的更为精确的估计。

IMU measurements 的融合主要是考虑到场景中没有texture或者相机被遮挡的情况。

因此，从visual odometry module 可以得到相机在局部坐标系中的位姿。
好了，实际上我们已经有了如下信息：

  1. stero 相机的左相机的图像
  2. 提取出来的Harris corners
  3. 相机的位姿

这三个东西要送到 landmark matching module。在这个module中，我们要为每一个 Harris corners 提取 HOG descriptor。
这样我们就得到了由四个部分组成的query landmark shot:

  1. the normalized 2D image coordinates
  2. 3D coordinates
  3. the HOG descriptors of the corner
  4. the camera pose

这个 query landmark shot 用于在 the landmark database 中搜索 potential similar landmark shots, 然后使用 image-based 2D matching来精简 potential landmark shot list。
找到matched landmark shot之后，就可以计算相机在全局坐标系中的坐标了。

由于matching直接用于确定全局坐标系中的坐标，因此必须对matching的质量严格把关，作者采用了a visual odometry trajectory based consistency check。

matching之后，由于 landmark matching 可能存在误差，因此需要将这一步估计出来的全局坐标系下的位姿送到一个 global localization module 中，来进一步估计全局坐标。

Efficient Landmark Matching with Disk-Cache Mechanism

略过

Local Visual Odometry Trajectory Based Consistency Check

为了提高定位的 robustness，从 matched landmarks 计算出来的 pose 要先和 visual odometry 计算的pose进行对比，以去除any possible wrong matches，并对landmark matching 施加 temporal consistency。

怎么对比呢，绝对位姿没法比，相对位姿还是可以的。
假设一个对象从 A 点到达 B点，我们可以

  1. 从visual odometry模块得到一个 A B之间的相对位姿，
  2. 也可以从matching模块中，提高A，B 图像与landmark database中matching之后计算的位姿得到一个相对位姿。

在短时间内，我们认为 visual odometry得到的相对位姿更准确，因此如果这俩相对位姿比较一致，那么就认为matching就很good。

Kalman Filter Based Fusion for Global Localization

我们要估计每一帧在全局坐标系中的位置
这一步其实就是将IMU-based multi-stereo visual odometry module 估计得到的 local pose，
转换 到
从第一个成功的landmark matching估计得到的 global camera pose 所在的全局坐标系。

本文的基于 Kalman Filter 的 global pose estimation module 的输入为：

  1. the query landmark shot (2D)
  2. matched database landmark shot (3D)
  3. the estimated global camera pose of the query shot

然后，从 IMU-based multi-stereo visual odometry module 转换 得到的 global pose 再和Kalman filter得到的 global landmark point measurements 进行融合。

此处的 global landmark point measurements 怎么得到的呢？就是2D to 3D的特征点的匹配啦，即the query landmark shot中的特征点 和 matched database landmark shot 中的 3D local point cloud 进行匹配。

我们要使用 estimated global pose of the query shot，将 每一个 3D local landmark point ${\bf X}$, 转化到 全局坐标系。
将姿态表示为：\({\bf P}_{LG}=[{\bf R}_{LG},{\bf T}_{LG}]\)，那么 \({\bf X}\) 就可以按照如下方程进行转换：
\({\bf Y}={\bf R}_{LG}{\bf X}+{\bf T}_{LG}\)

在 small error assumption 的时候，上式可以表示为：
\(\hat{\bf Y}+\delta {\bf Y}\simeq ({\bf I}-[{\mbi \rho}]_{\times}) \hat{\bf R}_{LG}(\hat{\bf X}+\delta {\bf X})+ \hat{\bf T}_{LG}+\delta {\bf T}_{LG}\)

我不知道为啥这里是减号而不是加号。
这里的 $\rho$ 是一个小的旋转矢量。
上式展开，忽略掉二阶项之后就得到如下的 线性化 ：
\(\delta {\bf Y}\simeq \hat{\bf R}_{LG}\delta {\bf X}+\left[\hat{\bf R}_{LG} \hat{\bf X}\right]_{\times}{\mbi \rho}+\delta {\bf T}_{LG} \eqno{\hbox{(3)}}\)

令 \(\tilde{\bf X}=\hat{\bf R}_{LG}\hat{\bf X}\)。
那么 local 3D (landmark) point 的 协方差矩阵 ${\bf \Sigma}_{Y}$ 可以在全局坐标系中使用如下的项进行表示：

  1. local reconstruction uncertainty, ${\bf \Sigma}_{X}$,
  2. the weight factor of the query landmark shot, ${\mbi W}$, 并将其建模为 query landmark shot 和 matched landmark shot 之间的距离，它反映了landmark matching的精度。
  3. landmark pose uncertainty in rotation and translation, ${\bf \Sigma}R_{LG}$ and ${\bf \Sigma}T_{LG}$

即：
\({\bf \Sigma}_{Y}\simeq\hat{\bf R}_{LG}(W{\bf \Sigma}_{X})\hat{\bf R}_{LG}^{T}+ [\hat{\bf X}]_{\times} {\bf \Sigma}R_{LG} [\hat{\bf X}]_{\times}^{T}+ {\bf \Sigma}T_{LG}\)

将上述步骤应用到 successful landmark matching 的 所有的 point correspondences

然后使用下面文献的方法将所有的 point correspondences融合到Kalman filter中：

A. Mourikis and S. Roumeliotis. A multi-state constrained kalman filter for vision-aided inertial navigation. In IEEE Conference on ICRA’07, 2007. 81, 85